Anti-Instances in Haskell

Typeclass instances are a powerful tool for specifying which overloaded operations are allowed on which types. But what about specifying which operations are disallowed on which types? With the arrival of Unsatisfiable in GHC 9.8.1, Haskell has better answers now than ever before.

Anti-Instances: Past and Present

An anti-instance is the intentional rejection of a possible typeclass instance. Anti-instances can be defined implicitly by omission or explicitly by custom type error.

Omitted Instances

The easiest and most common method for disallowing a typeclass operation on a given type is simply not providing the corresponding typeclass instance.

As an example, let's look at omitted instances on Data.Semigroup.First:

newtype First a = First { getFirst :: a }

instance Semigroup (First a) where
    (<>) :: First a -> First a -> First a
    a <> _ = a

First comes with a Semigroup instance as (<>), an append operation obeying the associativity law¹, can be implemented for combining First values.

λ> First 99 <> First 12 <> First 30 <> First 7
First 99
λ> ((First 12 <> First 30) <> First 7) <> First 99
First 12
λ> First 12 <> (First 30 <> (First 7 <> First 99))
First 12

On the other hand, there is no Monoid instance provided for First. No value can be supplied to First that, when combined with a distinct second value, would result in the second value. Therefore mempty, an "empty" value satisfying the identity law¹, cannot be implemented for First.

Typeclass hierarchies help users quickly distinguish how different types behave by communicating the operations they implement and the laws they satisfy. Observing where different types fall within these hierarchies is an easy way to discover intentionally omitted instances.²

Figure 2: A typeclass hierarchy (Typeclassopedia)

Using TypeError

The 2016 release of GHC 8.0.1 introduced TypeError for custom compile-time errors. Unlike with omitted instances, TypeError enables explicit anti-instances:

{-# LANGUAGE GHC2021, DataKinds #-}

import GHC.TypeError (TypeError, ErrorMessage (Text))

class ReflexiveEq a where
    reflexiveEq :: a -> a -> Bool

instance TypeError
  (Text "Equality is not reflexive on Double: NaN /= NaN")
  => ReflexiveEq Double where
    reflexiveEq _ _ = False

Triggering a compilation error with the above anti-instance can be seen below:

λ> reflexiveEq (1 :: Double) (1 :: Double)

<interactive>:30:1: error: [GHC-64725]
    • Equality is not reflexive on Double: NaN /= NaN
    • In the expression: reflexiveEq (1 :: Double) (1 :: Double)

Custom type errors enable user-defined error messages and provide concrete pointers for code documentation and reference in discussions. TypeError improves developer experience by enhancing library accessibility, IDE tooltips, and user interactions with the compiler.

One downside of TypeError is its implementation as a type-level function.³ This provides flexibility but makes it more difficult to understand when exactly a TypeError will be thrown.

While TypeError usage has been minor within the Haskell ecosystem, there are some very cool examples of them appearing in several libraries.⁴

Introducing Unsatisfiable

The upcoming GHC 9.8.1 release will bring an improved version of TypeError called Unsatisfiable.

{-# LANGUAGE GHC2021, DataKinds #-}

import GHC.TypeError (Unsatisfiable, ErrorMessage (Text))

instance Unsatisfiable
  (Text "Halt! Functions cannot be compared for equality.")
  => Eq (a -> b)

Triggering a compilation error with the above anti-instance can be seen below:

λ> (\x -> x) == (\y -> y)

<interactive>:18:11: error: [GHC-22250]
    • Halt! Functions cannot be compared for equality.
    • In the expression: (\ x -> x) == (\ y -> y)

Anti-instances defined with Unsatisfiable look nearly identical to those defined with TypeError, but have some additional benefits. Unlike TypeError, Unsatisfiable is a typeclass and thus produces types of kind Constraint.

λ> :kind TypeError
TypeError :: ErrorMessage -> b
λ> :kind Unsatisfiable
Unsatisfiable :: ErrorMessage -> Constraint

This results in more predictable error reporting and fixes buggy behavior seen when TypeError is used with -fdefer-type-errors. You can find more details on its advantages in the Unsatisfiable GHC Proposal.

Tips & Tricks

Escape Hatch

What if you really need an operation from an outlawed instance? Whether facing an implicit anti-instance by omission or an explicit anti-instance by custom type error, the solution is to use a newtype.

Newtypes overcome anti-instances by creating a wrapper type upon which fresh instances can be created without polluting the underlying type.

For example, we can implement a Monoid instance on UnsafeFirst without worrying about the Monoid anti-instance on First:

{-# OPTIONS_GHC -fno-warn-orphans #-}
{-# LANGUAGE GHC2021, DataKinds #-}

import Data.Semigroup (First)
import GHC.TypeError (Unsatisfiable, ErrorMessage (Text))

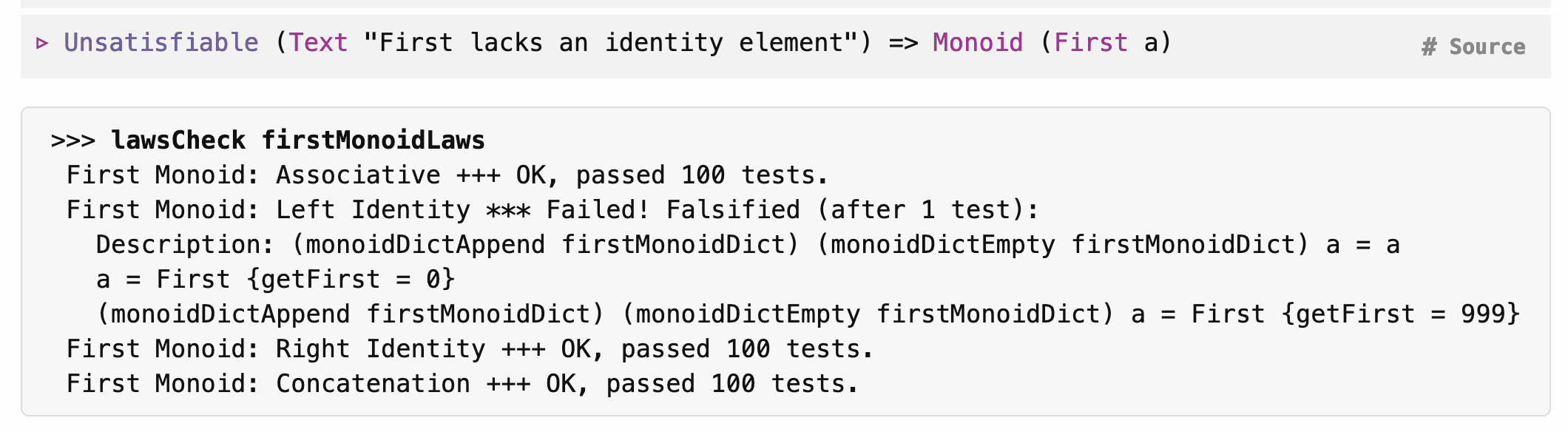
instance Unsatisfiable (Text "First lacks an identity element")
   => Monoid (First a)

-- | `First`, but with a `Monoid` instance
newtype UnsafeFirst a = UnsafeFirst
  { getUnsafeFirst :: First a }
  deriving (Show, Semigroup)

instance Monoid (UnsafeFirst a) where
  mempty :: UnsafeFirst a
  mempty = error "certified law breaker"

This "works":

λ> UnsafeFirst (First 1) <> UnsafeFirst (First 3)
UnsafeFirst {getUnsafeFirst = First {getFirst = 1}}
λ> UnsafeFirst (First 1) <> mempty
UnsafeFirst {getUnsafeFirst = First {getFirst = 1}}

...at least until there's a law-breaking mempty in the first position.

λ> mempty <> UnsafeFirst (First 3)
UnsafeFirst {getUnsafeFirst = First
  {getFirst = *** Exception: certified law breaker
CallStack (from HasCallStack):
  error, called at <interactive>:52:12 in interactive:Ghci7

Clearly, the above example is a bad idea. Carefully consider whether this workaround is a good idea and truly necessary in your case. There's likely a different representation of your data that can better achieve your goals.

For example, a different First datatype exists in Data.Monoid that wraps the Maybe datatype.

newtype First a = First { getFirst :: Maybe a }

instance Semigroup (First a) where
  (<>) :: First a -> First a -> First a
  First Nothing <> b = b
  a             <> _ = a

instance Monoid (First a) where
  mempty :: First a
  mempty = First Nothing

Combining values under Data.Semigroup.First means selecting the first value, while combining values under Data.Monoid.First means selecting the first "non-empty" value.

λ> First Nothing <> First Nothing <> First Nothing
First {getFirst = Nothing}
λ> ((First Nothing <> First (Just 99)) <> First Nothing) <> First (Just 33)
First {getFirst = Just 99}
λ> First Nothing <> (First (Just 99) <> (First Nothing <> First (Just 33)))
First {getFirst = Just 99}

Verified Counterexamples

One of Haskell's strengths is its facility for making assumptions explicit.⁵ Rather than implicitly omitting impossible instances, Haskellers can communicate intent with anti-instances. Further, claims about why an anti-instance exists can be strengthened by incorporating machine-checked validations.

Using property-based testing with doctests, we can verify typeclass instances and anti-instances directly in our documentation. The presence of counterexamples from generated values makes it clear which anti-instances are legitimately law-breaking. Likewise, the absence of counterexamples from generated values makes it clear which typeclass instances are legitimately law-abiding.

Further Reading

For more on this topic, I highly recommend reading the Unsatisfiable GHC Proposal and A story told by Type Errors.

Additionally:

• For learners looking to level up their typeclass knowledge...

  Advanced beginners and intermediate Haskellers looking to deepen their understanding of typeclasses and type-level techniques should check out Thinking With Types for a comprehensive tour. Other resources I've found interesting and useful include:

  • Code Reuse in PureScript: Fns, Classes, and Interpreters (video)
  • Coherence of Type Class Resolution (video)
  • All You Wanted to Know About Type Classes (video)
  • An introduction to typeclass metaprogramming
• For more seasoned explorers...

  Those with further interest in this area:

  • See related GHC proposals like the recently accepted Deprecated Instances proposal and pending Custom Type Warnings proposal.
  • For why typeclass laws require manual verification, see Rice's theorem and this StackOverflow answer. See the Verifying replicated data types and Quotient Haskell papers for examples using Liquid Haskell to statically verify typeclass laws and encode laws directly onto datatypes, respectively.

If there's further interest, I may write more on this topic. I have some thoughts to flesh out around tradeoffs, related proposals, more ergonomic law-checking, and deriving anti-instances.

Thanks for reading!

✌️

Footnotes